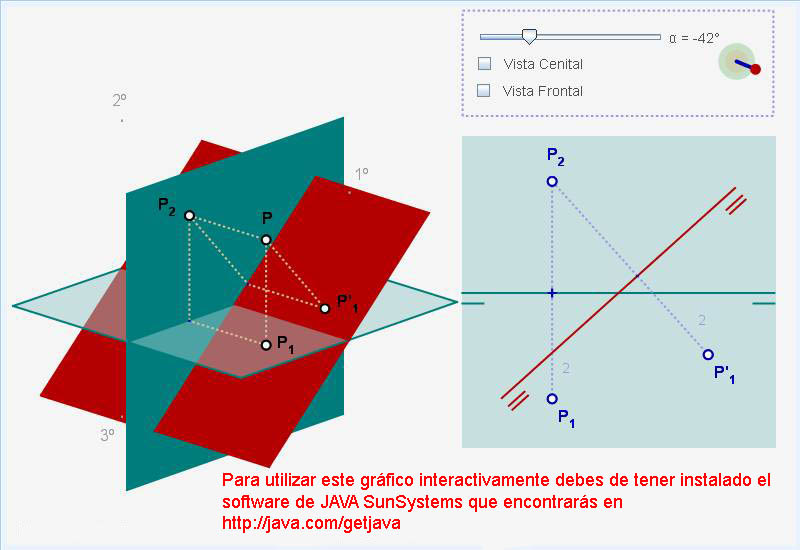
Caso del Sistema Axonométrico en el que los ejes forman entre sí dos ángulos iguales y uno desigual.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
domingo, 11 de septiembre de 2011
Diedro
Un ángulo diedro es cada una de las dos partes del espacio delimitadas por dos semiplanos que parten de una arista común. Es un concepto geométrico ideal, y sólo es posible representarlo parcialmente, como dos rectángulos con un lado común, que simbolizan dos semiplanos.
http://es.wikipedia.org/wiki/Diedro
http://es.wikipedia.org/wiki/Diedro
Diámetro
El diámetro de una circunferencia es el segmento que pasa por el centro y sus extremos son puntos de ella. Es la máxima cuerda (segmento entre dos puntos de la circunferencia) que se encuentra dentro de una circunferencia, o en un círculo. Todo diámetro divide a un círculo en dos semicírculos.
El diámetro de una esfera es el segmento que pasando por el centro, tiene sus extremos en la superficie de esta.
Desarrollo
Dícese de la forma resultante de la conversión por aplanamiento de una forma plana tridimensional en otra bidimensional.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Croquis
Un croquis es un dibujo que esboza una imagen o una idea, confeccionados con instrumentos de dibujo o copiado de un modelo, después de haber aprobado el boceto preelimninar. Generalmente, suele ser muy exacto y a veces sólo es legible para el autor.
Los croquis de un modelo son dibujos hechos a partir de un objeto, como un molde de plástico, arcilla, u otro material sólido. Algunos son de modelos de animales, paisajes, montañas, mares, ríos, o regiones geográficas.
También se consideran croquis, según el DRAE, el "diseño ligero de un terreno, paisaje o posición militar, que se hace a ojo y sin valerse de instrumentos geométricos".1
Cuerda
Una cuerda de una curva es un segmento geométrico, cuyos extremos se encuentran en la curva. La extensión lineal de una cuerda es unasecante.
Entre las propiedades de las cuerdas de un círculo se encuentran las siguientes:
- Las cuerdas son equidistantes del centro si y solo si sus longitudes son iguales.
- Una bisectriz de una cuerda pasa por el centro.
- Si las extensiones lineales (líneas secantes) de las cuerdas AB y CD se interceptan en un punto P, entonces sus longitudes satisfacen AP·PB = CP·PD, (ver potencia de un punto).
- La cuerda de mayor longitud posible para un determinado círculo es su propio diámetro.
El área que corta una cuerda circular es denominada un segmento circular.
Cubo
Un cubo o hexaedro regular es un poliedro de seis caras cuadradas congruentes, siendo uno de los llamados sólidos platónicos.
Un cubo, además de ser un hexaedro, puede ser clasificado también como paralelepípedo, recto y rectángulo, pues todas sus caras son de cuatro lados y paralelas dos a dos, e incluso como un prisma de base cuadrangular y altura equivalente al lado de la base.
El hexaedro regular, al igual que el resto de los sólidos platónicos, cumple el Teorema de poliedros de Euler, pues tiene seis caras, ocho vértices y doce aristas (8+6=12+2).
Cota
Cifra que indica una dimensión en general. "Cota de un punto": coordenada "z" que expresa la distancia de un punto al plano horizontal de proyección.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Corte
Convencionalismo gráfico que permite la visualización directa de oquedades en piezas al quedar al descubierto, de manera que se clarifique su estructura interna.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Coordenadas cartesianas
El Sistema cartesiano es un sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) x e y se denominan abscisa yordenada, respectivamente.
http://es.wikipedia.org/wiki/Coordenadas_cartesianas
http://es.wikipedia.org/wiki/Coordenadas_cartesianas
Cono
Cono:
Porción de superficie cónica comprendida entre el vértice y un plano cualquiera. (Véase superficie cónica).
a) Recto: el eje es perpendicular al plano de la base.
b) Oblicuo: el eje no es perpendicular al plano de la base.
c) Truncado: cuando es cortado por un plano, definiendo una segunda base.
a) Recto: el eje es perpendicular al plano de la base.
b) Oblicuo: el eje no es perpendicular al plano de la base.
c) Truncado: cuando es cortado por un plano, definiendo una segunda base.
Concurrente
Dícese del elemento que se junta o coincide con otro, en un mismo lugar. (los lados de un ángulo, son dos rectas concurrentes, que coinciden o se juntan en el vértice de dicho ángulo).
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Concéntrico
Dícese del elemento geométrico que tiene el mismo centro que otro.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Coaxial
Dícese del elemento geométrico que tiene el mismo eje que otro.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Circunferencia
Una circunferencia es el conjunto de todos los puntos de un plano que equidistan de otro punto fijo y coplanar llamado centro.
A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
http://es.wikipedia.org/wiki/Circunferencia
A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
http://es.wikipedia.org/wiki/Circunferencia
Círculo
Un círculo, en geometría, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que la longitud del radio. Es el conjunto de los puntos de un plano que se encuentran contenidos en una circunferencia.
En castellano, la palabra círculo tiene varias acepciones, la primera:1 una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia2 a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud. "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)."3
Cambio de plano
Es el mecanismo de proyectar sobre un plano diferente a un coordenado, con objeto de obtener una visión más favorable del elemento representado.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Caballera
Perspectiva basada en la proyección cilíndrica oblicua sobre un triedro trirrectángulo en el que el plano XZ queda frontal al observador.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Bisectriz
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirrectas de un ángulo.
http://es.wikipedia.org/wiki/Bisectriz
http://es.wikipedia.org/wiki/Bisectriz
Axonométrico
Sistema de representación que utiliza como base de proyección un triedro trirrectángulo. Este sistema posee tres variantes: Isométrico, Dimétrico y Trimétrico. (Véanse las correspondientes definiciones en este Vocabulario).
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Arco
En geometría, arco es cualquier curva continua que une dos puntos.1 También, se denomina arco a un segmento de circunferencia; un arco de circunferencia queda definido por tres puntos, o dos puntos extremos y el radio, o por la longitud de una cuerda y el radio.
http://es.wikipedia.org/wiki/Arco_(geometr%C3%ADa)
http://es.wikipedia.org/wiki/Arco_(geometr%C3%ADa)
Ángulo complementario
Es aquel cuya medida se corresponde con lo que le falta a otro para medir un ángulo recto. La suma de dos ángulos complementarios es otro de 90º.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Ángulo Agudo
Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de  rad.
rad.
 rad.
rad.Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales).
Ángulo
Es la porción de plano limitado por dos semirrectas, llamadas lados, que parten de un mismo punto llamado vértice. En el espacio se define como: la porción de espacio limitado por dos semiplanos, llamados caras, que parte de una recta común, llamada arista.
Alzado
En la representación de una pieza por vistas, dícese de la vista principal. Es la más representativa de la misma, la que nos da una mejor idea de su forma y proporciones.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Alejamiento
Coordenada "y" que expresa la distancia de un punto al plano vertical de proyección.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Acotación
Acción de acotar o colocar medidas en la representación de un objeto (según normativa) de manera que su forma y dimensiones queden perfectamente determinadas.
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
http://almez.pntic.mec.es/~ssar0003/diccionario.htm
Suscribirse a:
Comentarios (Atom)




_of_roller_chain,_Leonardo_da_Vinci.jpg)